近年来,随着机器人技术的迅速发展,机器人在工业、医疗、军事等领域的应用越来越广泛。机器人轨迹规划是机器人控制的重要环节之一,它决定了机器人在执行任务时的运动轨迹,直接影响机器人的精度、速度和稳定性。因此,机器人轨迹规划算法的研究一直是机器人领域的热点和难点之一。
机器人轨迹规划算法主要分为笛卡尔空间轨迹规划和关节空间轨迹规划两类。笛卡尔空间轨迹规划是指在笛卡尔坐标系下,确定机器人末端执行器的运动轨迹。关节空间轨迹规划是指在关节空间下,确定机器人各个关节的运动轨迹。下面将分别介绍这两种轨迹规划算法的研究现状。
笛卡尔坐标系是一种二维或三维坐标系,以直角坐标系为基础,通过描述机器人的位置和姿态实现机器人的运动控制。在笛卡尔空间下,机器人的运动可以用平移和旋转两个自由度描述,其中平移自由度包括机器人的位置信息,旋转自由度包括机器人的姿态信息。笛卡尔空间轨迹规划是机器人轨迹规划中的一种常见方法,它主要用于末端执行器的运动轨迹规划。笛卡尔空间轨迹规划通常需要将任务要求转换为末端执行器的位置和姿态要求,然后通过插值或优化等方法,生成一条平滑的轨迹。
目前,研究者们对笛卡尔空间轨迹规划算法进行了广泛的探索和尝试,并提出了多种不同的算法。根据研究方法和求解过程的不同,可以将这些算法分为以下几类:
插值方法是一种较为简单但高效的轨迹规划方法,在笛卡尔空间下常用的插值方法包括直线插值、圆弧插值和样条插值。其中,直线插值方法是最为简单的一种,其思路是将原始的线段分段逼近为多个小线段,在每个小线段上进行加减速的规划,从而使机器人能够实现平滑的轨迹运动。圆弧插值方法则是在直线插值的基础上,将机器人的移动轨迹曲线化,从而实现更加自然、优美的运动效果。样条插值算法则是在曲线上对未知点进行插值计算,从而得到平滑的曲线轨迹规划。
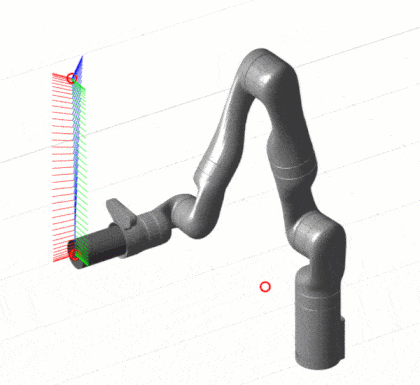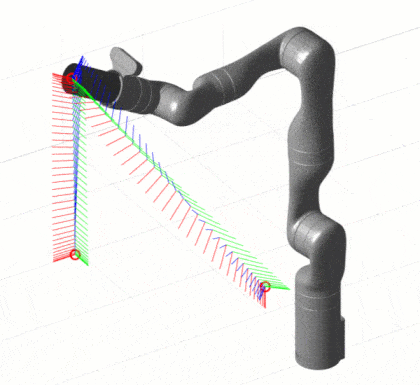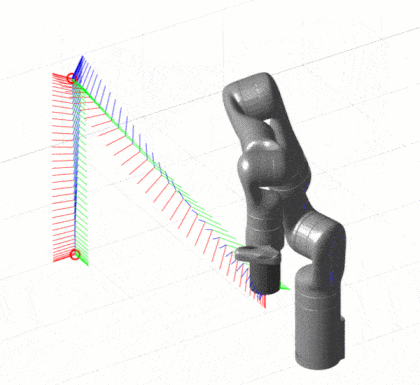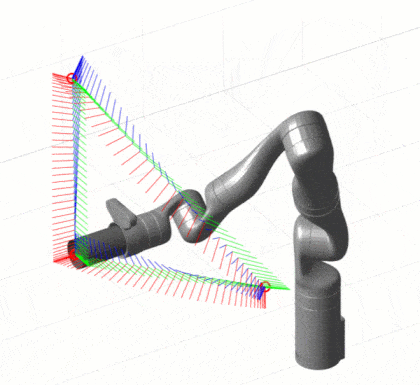
虽然插值方法具有简单高效的特点,但该方法并不能充分利用机器人系统的控制能力和优化思想。因此,在一些概率机器人和机器人学领域中,研究者们开始使用基于优化的轨迹规划算法。这类算法的思想是通过优化目标函数,寻找机器人在笛卡尔空间中的最佳运动轨迹。常见的基于优化方法的轨迹规划算法有遗传算法、模拟退火算法、粒子群算法等。
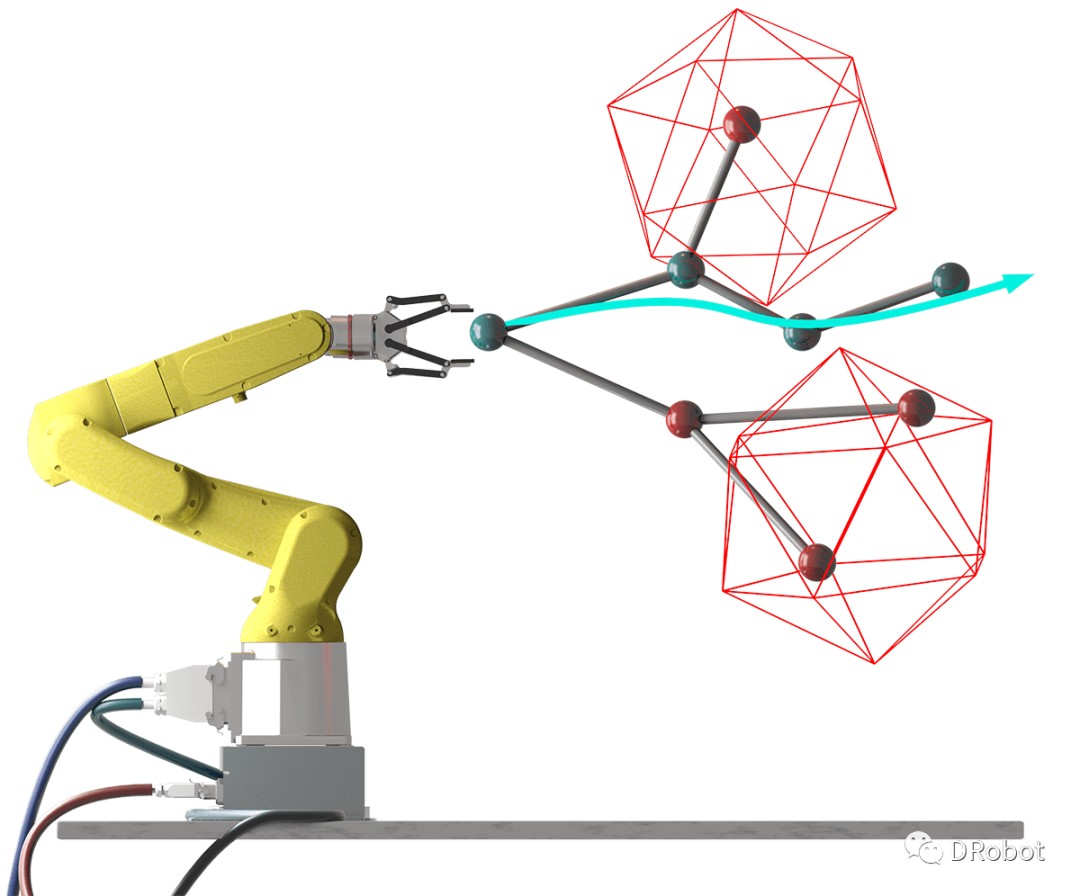
近年来,人工智能技术的发展为机器学习方法的应用提供了新的空间。机器学习方法可以通过对数据进行训练和学习,从而得到模型的拟合方程,并实现更为准确的轨迹规划效果。常见的基于机器学习的轨迹规划算法有神经网络算法、支持向量机算法、决策树算法等。
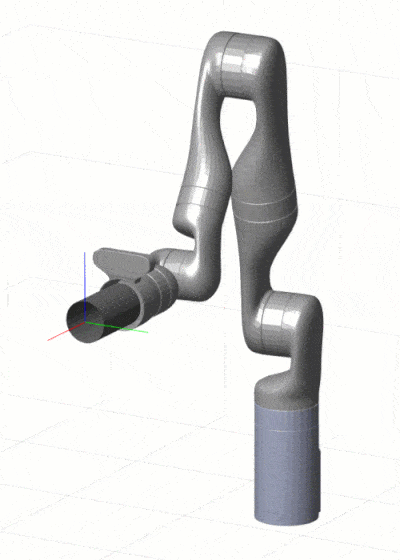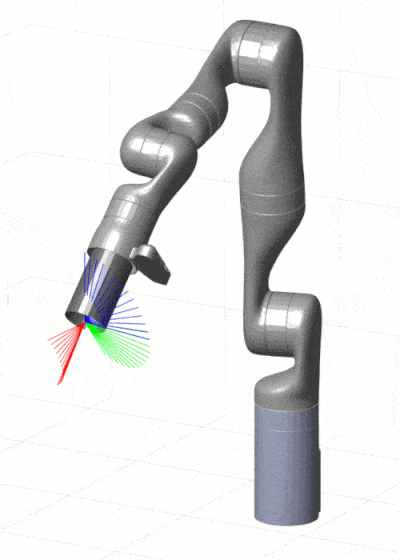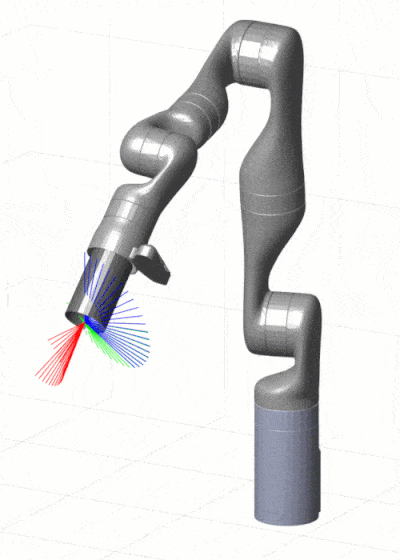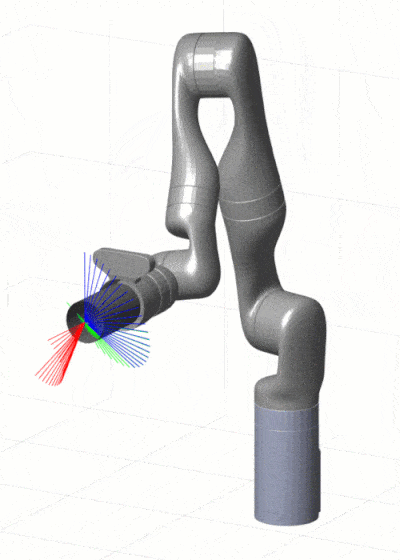
虽然在笛卡尔空间轨迹规划领域中已经涌现出多种不同的算法,但每种算法都有其优缺点和适用范围。直线插值算法虽然简单高效,但其计算精度难以保证;而圆弧插值算法可以实现曲线轨迹规划,但需要考虑曲率问题,运动轨迹更难控制。基于优化方法的算法能够规划出机器人的最优运动轨迹,但其耗时较长,计算复杂度较高。机器学习方法可以获得更高的计算精度和规划效果,但需要大量数据进行训练和学习,且计算时间较长。在未来的研究中,还可以将多种算法进行融合,并实现算法的优势互补,以便更好地解决笛卡尔空间轨迹规划问题。
关节空间轨迹规划是机器人轨迹规划中的另一种常见方法,它主要用于关节的运动轨迹规划。关节空间轨迹规划通常需要考虑机器人的运动学和动力学特性,以及关节的限制条件,然后通过插值或优化等方法,生成一条平滑的轨迹。
插值算法是关节空间轨迹规划中最常用的方法之一。它通过对给定的关节角度进行插值,生成一条平滑的轨迹。常见的插值算法包括多项式插值、样条插值、优化插值等。
多项式插值是关节空间轨迹规划中最简单的方法之一,它通过对给定的关节角度进行多项式逼近,生成一条平滑的轨迹。在每个点的位置和导数值相同的情况下,可以通过多项式插值来生成一条平滑的轨迹。
样条插值是一种基于多项式的插值算法,它可以生成一条光滑的轨迹,适用于连续的轨迹规划。样条插值的基本思想是将整个轨迹分成多个小段,每个小段用一个低次数的多项式来逼近。在每个小段的连接处,要求多项式的一阶导数和二阶导数连续,以保证整条曲线的光滑性。
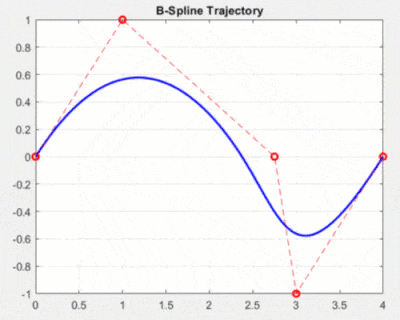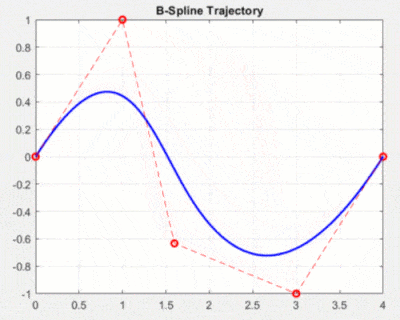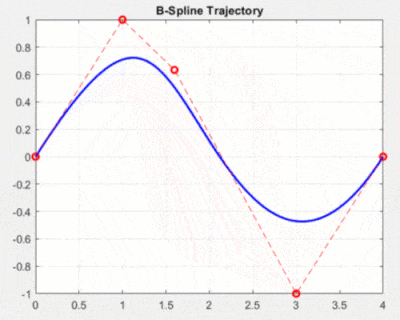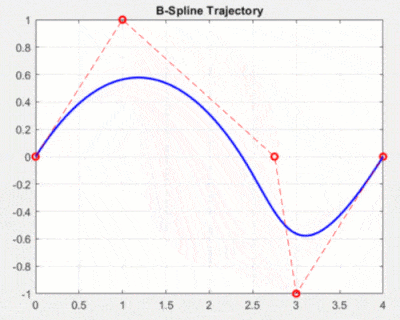
优化插值是一种基于优化的插值算法,它通过建立优化模型,利用数学优化方法来生成一条平滑的轨迹。在关节空间轨迹规划中,优化插值可以通过不断调整关节角度的参数,来生成一条平滑的轨迹。
优化算法是关节空间轨迹规划中另一种常用的方法。它通过建立优化模型,利用数学优化方法来生成一条平滑的轨迹。常见的优化算法包括基于梯度下降的优化算法、基于遗传算法的优化算法、基于粒子群算法的优化算法等。
基于梯度下降的优化算法是一种基于局部搜索的优化算法,它通过计算目标函数的梯度方向,不断调整关节角度的参数,使得目标函数最小化。在关节空间轨迹规划中,目标函数通常是轨迹的长度或者曲率,通过不断调整关节角度的参数,可以使得轨迹变得更加平滑。
基于遗传算法的优化算法是一种基于全局搜索的优化算法,它通过模拟自然界的进化过程,不断生成新的关节角度,并筛选出最优的关节角度。在关节空间轨迹规划中,遗传算法可以通过不断生成新的关节角度,来生成一条平滑的轨迹。
基于粒子群算法的优化算法是一种基于群体智能的优化算法,它通过模拟鸟群或鱼群的行为,不断调整关节角度的参数,使得目标函数最小化。在关节空间轨迹规划中,粒子群算法可以通过不断调整关节角度的参数,来生成一条平滑的轨迹。
启发式算法是一种计算效率高、适用广泛的算法,它适用于复杂的非线性问题。基于启发式算法的方法主要包括搜索算法、模拟退火算法、神经网络算法、粒子群算法等。这些算法最初是在优化问题中出现的,但是由于其简单而又高效的特点,在路径规划问题中也得到了广泛的应用。
机器人轨迹规划算法是机器人控制的重要环节之一,它决定了机器人在执行任务时的运动轨迹,直接影响机器人的精度、速度和稳定性。笛卡尔空间轨迹规划和关节空间轨迹规划是机器人轨迹规划中的两种常见方法。笛卡尔空间轨迹规划通常需要将任务要求转换为末端执行器的位置和姿态要求,然后通过插值或优化等方法,生成一条平滑的轨迹。关节空间轨迹规划通常需要考虑机器人的运动学和动力学特性,以及关节的限制条件,然后通过插值或优化等方法,生成一条平滑的轨迹。未来,随着机器人技术的不断发展,机器人轨迹规划算法也将不断完善和创新,为机器人应用提供更加高效和可靠的支持。