在各大品牌的摄影镜头中，鱼眼镜头焦距极短，视场角极广，与野生动物摄影师的天然工具——长焦镜头截然相反。迄今为止，我从未有机会使用过这种能够拍摄整个半球的神奇镜头，出于好奇，我决定了解一下它们的工作原理。因此，本页面只是一些整理过的学习资料，方便大家阅读。作为尼康相机的用户，我自然而然地将注意力集中在这家制造商的鱼眼镜头上。

目前，尼康目录中列出了两款“全画幅”鱼眼镜头：

• 10.5 毫米 f/2.8 覆盖 15.8 x 23.6 毫米画幅（Dx），
• 16 毫米 f/2.8 覆盖 24 x 36 毫米画幅。

该品牌最后两款“圆形画幅”鱼眼镜头——气势恢宏的 6 mm f/2.8 Ais 和 8 mm f/2.8 Ais，在 2000 年前不久停产。6 mm f/2.8 拥有 220° 的视场角，其工作原理对我来说一直是个谜。我甚至认为这款气势恢宏的镜头是广角镜头所能达到的极限。但我的研究表明，我错了……

10.5 毫米 f/2.8 和 16 毫米 f/2.8，均为尼康当前的鱼眼镜头（尼康文件）。

• 1 鱼眼镜头与其他镜头不同
• 2 AF Dx 鱼眼尼克尔 10.5 mm f/2.8G ED。
• 3 AF 鱼眼尼克尔 16 mm f/2.8D。
• 4 鱼眼尼克尔 6 mm f/2.8。
• 5 本可以是“Fisheye-Nikkor 5.4 mm f/5.6”的镜头。

1 鱼眼镜头与其他镜头不同

鱼眼镜头与其他镜头有何不同？

这个问题的答案或许是“它们的 180 度视场角”（甚至更大）。嗯，我更倾向于认为，它们的“映射函数”才是它们的与众不同之处……

关于这个映射函数只需说几句话：

在相机的传感器上，物点图像的位置取决于：

• 光轴与入射光束（从物点）之间的角度
• 镜头的焦距
• 镜头的映射函数

图 1（下图）展示了一个以“经典方式”工作的镜头示例：它的映射函数通常被称为“透视投影”或“球面投影”。几乎所有镜头都是根据这一原理设计的（或或多或少倾向于满足这一原理）。这也是针孔相机的映射函数。

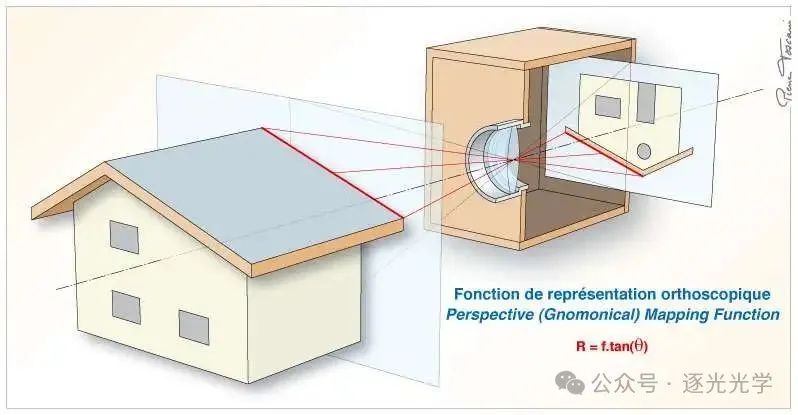
图 1： 通过透视投影获得的图像。

理论上，该映射函数可以将场景中的所有直线用直线重现到图片上。因此，理论上图片上不会出现畸变（不要将其与透视畸变混淆，因为如果线条忠实地呈现，则线条之间的角度不会失真）。

然而，视场角超过 110° 且适用于单反相机（长后焦距）的透视投影镜头的设计相当困难。为了实现这一点，必须制造焦距极短的光学系统，而这些系统非常复杂，因此成本也非常高昂。

从数学上讲，透视投影表示如下：

其中，

•  是“径向距离”，即图像中心（光轴与传感器相交处）与像点之间的距离
•  是镜头的焦距
•  是光轴与入射光束（来自物点）之间的角度

按照此原理工作的镜头的操作限制非常明确：为了在给定 R 值的情况下实现 180° 的视场（ = 90°），焦距必须趋近于零。 这就是问题所在……

图 2（下图）说明了这些因素在图像形成过程中的作用。左图显示，径向距离  随角度 （红色曲线）的增大而快速增加。本例使用 15 毫米透视投影镜头。因此，当角度 Theta = 45° 时，对应的径向距离 R = 15 毫米。在传感器（右图）上，所有 45° 入射光束都会形成一个半径为 15 毫米的圆，无法完全进入 24 x 36 毫米的框架。

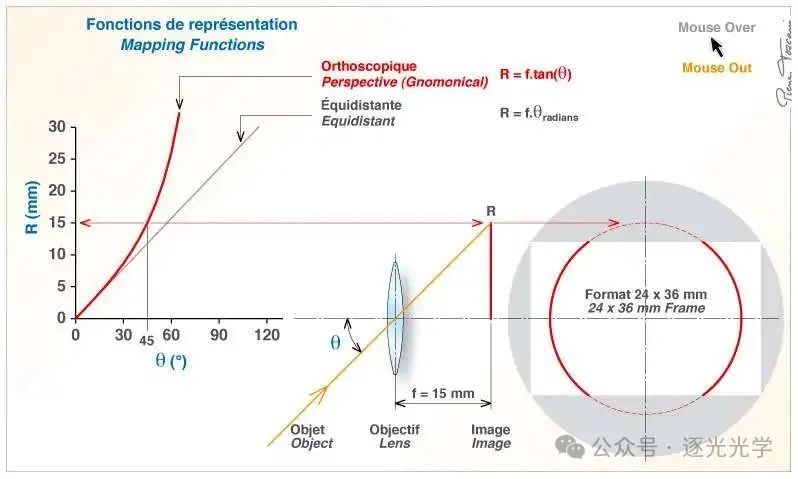
图 2 ： 映射函数。

为了克服透视投影的局限性，人们设计了具有其他映射函数的光学系统。这些替代函数的目的是“缩小”位于视场角边缘的物体图像，以便在保持实际焦距值的同时增加  角。换句话说，在这样的光学系统中，放大倍数在整个画面上并不恒定：边缘处的放大倍数低于中心处的放大倍数。 这正是鱼眼镜头与其他镜头的不同之处。

在几种映射函数中，鱼眼上使用最频繁的有两种函数：

• 等距函数

以弧度为单位

 

• 等立体角函数

理论上，表达式为 ，但实际上这两个系数都是特定于每个鱼眼的。

尽管等距函数不像等立体角函数那样常用，但它更容易进行角度测量。

当角度 Theta = 45° 时，15 毫米等立体角投影鱼眼的径向距离 R = 11.5 毫米。因此，在传感器（右侧）上，所有 45° 入射光束都描绘出一个半径为 11.5 毫米的圆，完美契合 24 x 36 毫米的框架。但随之而来的是桶形畸变，所有不与光轴相交的直线都会被还原成曲线。

与等立体角投影不同，等距投影是线性的。因此，它对图像边缘的压缩较小。

为了量化等立体角鱼眼的“畸变”，我们经常将其投影曲线与相同焦距的等距鱼眼的投影曲线进行比较。

2 AF Dx 鱼眼尼克尔 10.5 mm f/2.8G ED。

以下插图取自水口先生于 2007 年 1 月 9 日提交的美国专利 7,161,746 B2 的数据。本文件是对美国专利 6,844,991 B2（2005 年 1 月 18 日）的补充。镜头的光学系统由以下数据表完整定义（两专利相同 -示例 9 – 图 17）。

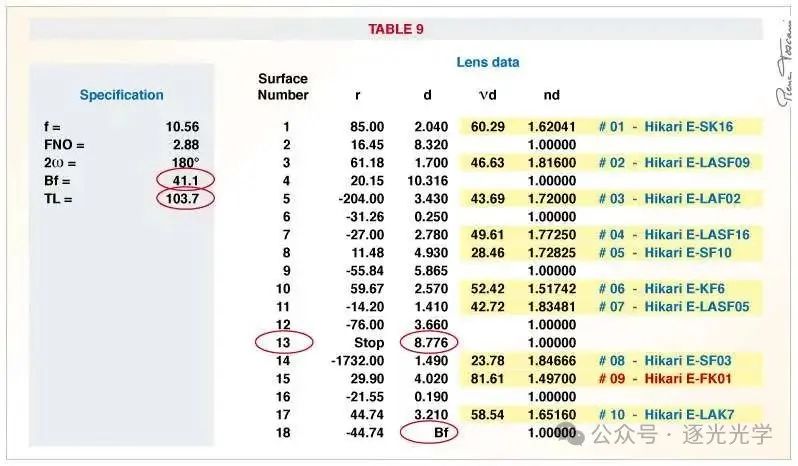
图3 ： AF DX Fisheye-Nikkor 10.5mm f/2.8G ED。光学系统定义（黑色数据取自美国专利 7,161,746 B2）。

但请注意，总光学长度 TL = 103.7 毫米（左下角）与 d 列间隔加上后焦距 Bf 之和不匹配。此外，计算结果表明，d13 = 8.776 毫米的值与后焦距 Bf = 41.1 毫米的值不匹配。事实证明， d13 值对应于对焦距离为 140 毫米时的光学系统配置，但此时 Bf 应该为 42.1 毫米（而不是 41.1 毫米）。因此，当镜头对焦于无限远时，d13 应该为 6.467 毫米。这是故意造成的误差吗？

该镜头所有镜片均为球面，仅有一片（#09）镜片采用了低色散玻璃 E-FK01（阿贝数为 81.61）。

这款小型镜头的成像直径为 28.4 毫米，覆盖 15.8 x 23.6 毫米画幅（尼康 DX），视场角为 182.6°（180° 视场角对应像圈直径 28.2 毫米）。

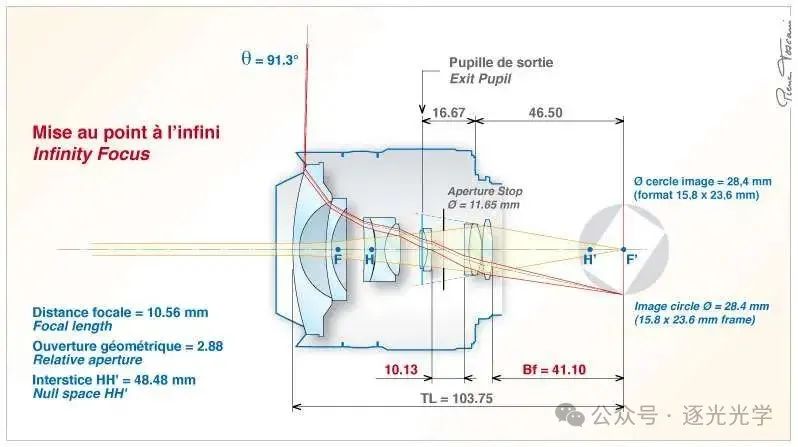
图4 ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。简化剖面图（全开光圈，无限远对焦）。请注意 θ = 0° 和 θ = 91.3° 时照明开口锥体的不同（光学渐晕）。

加上遮光罩（一种永久性的改变，通常被称为“shaved” lens），这款鱼眼镜头或许也会吸引 24 x 36 毫米传感器相机用户。这样一来，视场角将超过 200°（代价是成像圈边缘会出现明显的场曲）。在 200° 视场角下，成像圈直径达到 29.5 毫米。实际上，由于镜框高度（24 毫米），垂直方向的视场角限制在 142°。

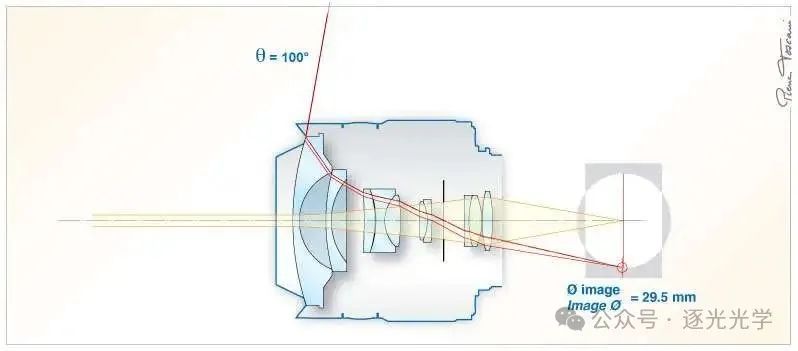
图 5 ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。图像形成于 24 x 36 毫米传感器上。

该镜头的最小焦距为 140 毫米（5.5 英寸）；拍摄对象仅位于前镜头前方 33 毫米（1.3 英寸）。

这款镜头的对焦由 CRC（近距校正）系统完成。当焦距从无限远变化到 140 毫米时，整个光学系统会向前移动（与往常一样），从而增加后焦距，但此时位于光圈前方的移动镜片的距离（3.3 毫米）是位于光圈后方的镜片距离（1 毫米）的三倍。这是一种无论焦距如何都能保持良好场平面度的方法。

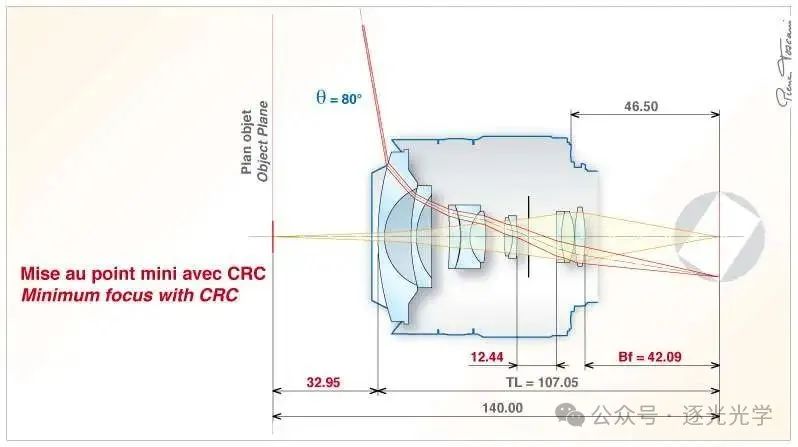
图6 ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。简化剖面，全开，对焦于 140 毫米（带 CRC 系统）。

这套 CRC 系统并非简单的广告噱头。它的效果是完全合理的，而且效果显著。为了说明其有效性，我比较了两束入射角  = 80° 的光束，在最小焦距、全开光圈、开启和关闭 CRC 的情况下的光线追踪。

• 第一种情况（上图 6）。镜头采用标准配置，使用 CRC 系统聚焦于 140 毫米处。斜光束（红色）正确聚焦于像平面。
• 第二种情况（下图 7）。无限远对焦配置下的镜头整体前移，实现 140 毫米对焦（未使用 CRC 系统）。斜光束（红色）在传感器前聚焦：物面仅在画面中心清晰可见。

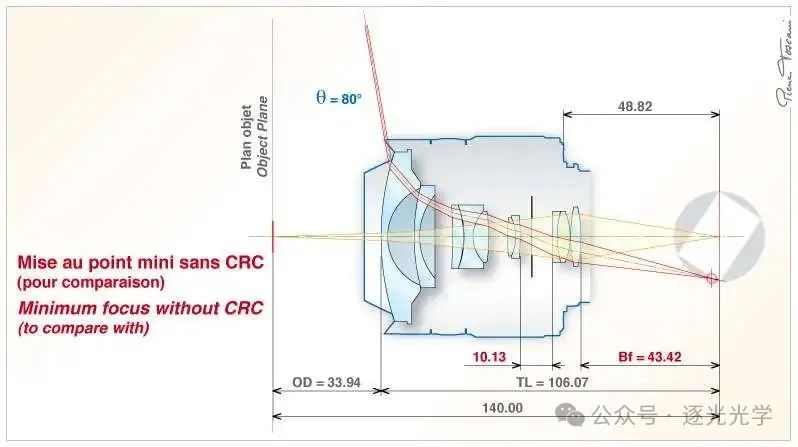
图7 ： AF DX Fisheye-Nikkor 10.5mm f/2.8G ED。未使用CRC系统时（对焦于140mm）的场曲率突出显示。

关于入瞳，我只想说几句话……

镜头入瞳的位置决定了其透视中心（无视差点）。小视场角镜头的入瞳可以视为一个固定点。然而，由于入瞳位置取决于光轴与入射光束之间的夹角，因此对于超广角镜头，无法定义单个无视差点。对于鱼眼镜头，大离轴角光束的入瞳位置比轴上光束的入瞳位置更靠前。

从孔径光阑的上下边缘（在子午面内）进行反向光线追踪，可以精确确定入瞳位置。图 8（下图）展示了该图应用于尼克尔 10.5 mm f/2.8 镜头的示例。光圈特意设置为 f/8，以消除光学渐晕效应。入射角  = 80° 的入射光束的入瞳位于轴向光束入瞳前方 11.8 mm，距离光轴 16.3 mm。它还向后倾斜 30°。

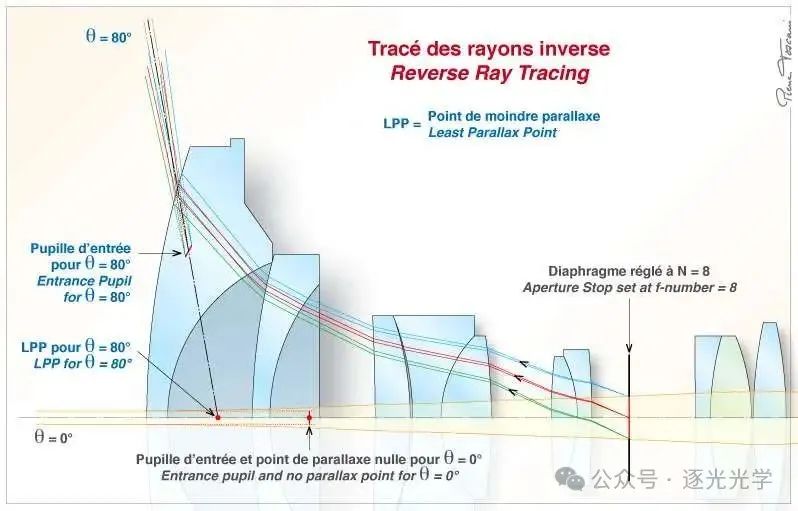
图 8 ：从光圈光圈反向追踪的光线，应用于AF DX Fisheye-Nikkor 10.5mm f/2.8G ED 的光学系统。

图 9（下图）展示了当  角从 0° 变化到 90° 时，鱼眼尼克尔 10.5 mm f/2.8 镜头的入瞳位移。在此过程中，穿过入瞳中心的光线与光轴的交点（又称“最小视差点”）也会向前移动。

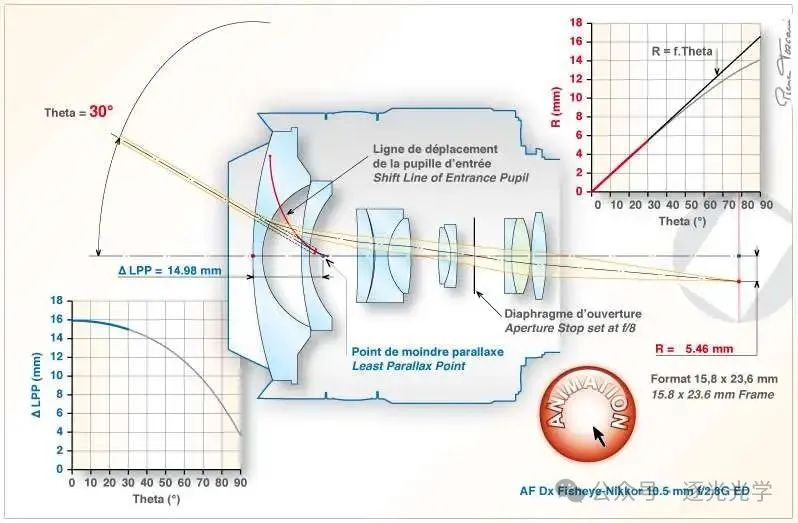
图 9 ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。入瞳位置与 Theta 角（无限远对焦）的关系。

全景照片要求图像在重叠区域由视差引入的误差最小。为了实现这一点，相机必须围绕与接缝角度位置相对应的最小视差点（即两张连续照片之间旋转角度的一半）旋转。

图 9a（下图）说明了当镜头围绕与入射角 Theta = 70° 相对应的最小视差点旋转时，两个物体的图像之间发生的视差误差的进展……A 和 B 是两个沿光轴完美排列的物体：在旋转镜头之前，A 和 B 的图像完美地叠加在传感器的中心。一旦镜头开始旋转，两个图像就会彼此远离（视差），因为它们会远离画面的中心，因为来自物体 A 和 B 的光束不会“看到”同一个入瞳。两个图像之间的间隙达到最大值，然后随着旋转角度接近 70° 而减小。最后，当达到 70° 值时，两个图像再次相遇（无视差）。超过此值时，视差会反转并再次增加，直到像场的最边缘。

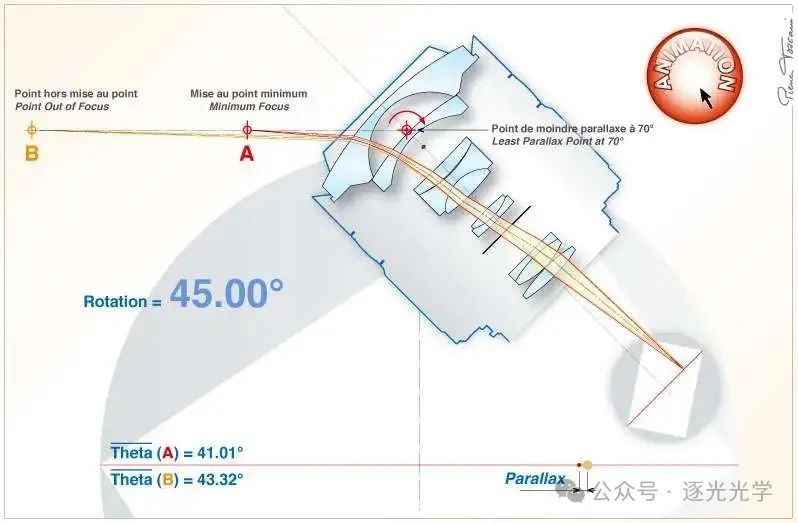
图 9a ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。突出显示两个完美对齐的物体图像之间出现的视差。

图 10 的图表显示了鱼眼尼克尔 10.5 mm f/2.8 最小视差点的计算投影、畸变和偏移。

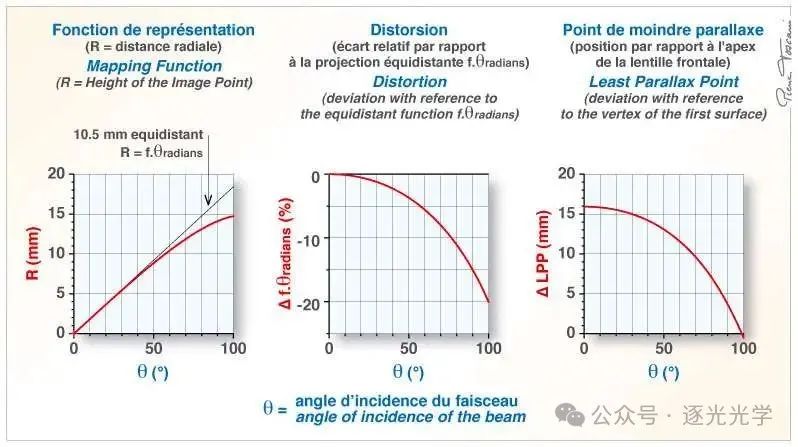
图 10 ： AF DX 鱼眼尼克尔 10.5mm f/2.8G ED。投影、失真和最小视差点位置（无限远对焦）。

该透镜的映射函数属于等立体角类型：

通过实验确定了  1.47 和  0.713。这些系数与上面的计算结果非常吻合（左图）。

3 AF 鱼眼尼克尔 16 mm f/2.8D。

以下插图取自 佐藤先生申请的美国专利号 5,434,713 （1995 年 7 月 18 日）。该镜头的光学系统很可能是尼康第一代 16 毫米鱼眼镜头之父清水先生发明的旧系统（美国专利号 3,734,600 – 1973 年 5 月 22 日）的改进版。下表列出了该镜头的光学系统（但未提及光圈的具体位置）。

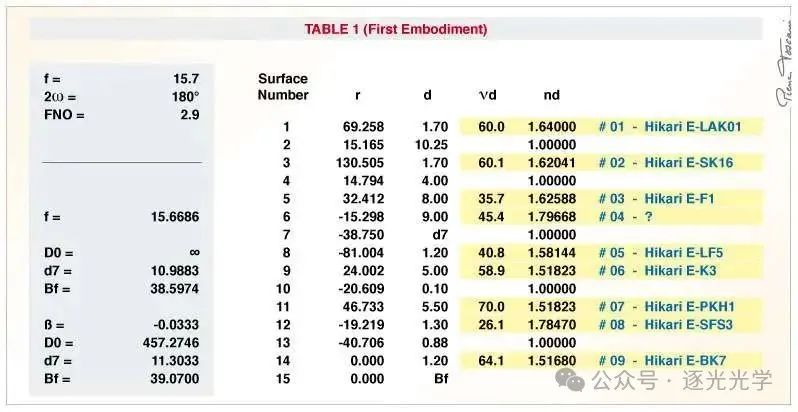
图11 ： AF Fisheye-Nikkor 16mm f/2.8D。光学系统定义（黑色数据取自美国专利5,434,713）。

该镜头没有低色散玻璃镜片（色散最小的玻璃镜片的阿贝数为 70）；所有镜片表面均为球面。将光圈设置在第四片镜片出射面后方 5.7 毫米处（根据 专利图 1 所示 ），43.3 毫米的像圈直径（24 x 36 毫米）覆盖的视场角略大于 180 度（180.56°）。

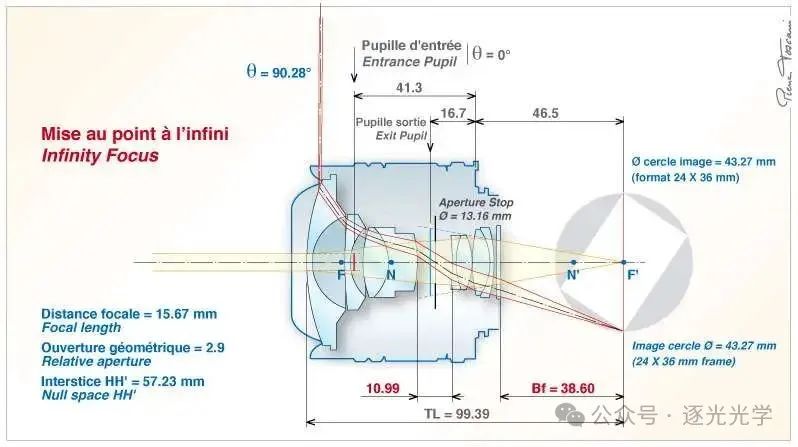
图 12 ： AF 鱼眼尼克尔 16mm f/2.8D。简化部分（全开光圈，无限远对焦）。

对焦采用与 10.5 毫米鱼眼镜头相同的 CRC 系统。最小焦距为 250 毫米（约 10 英寸）；此时拍摄对象位于前镜头前方 148 毫米（5.8 英寸）。

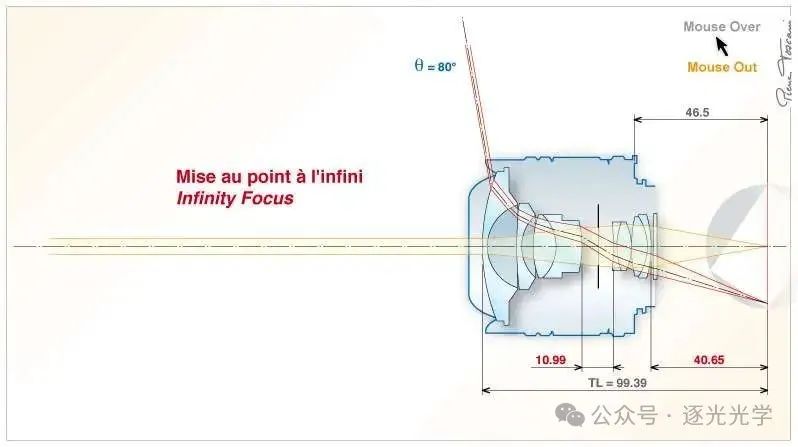
图 13 ： AF 鱼眼尼克尔 16mm f/2.8D。全光圈下的简化剖面图。鼠标移开：无限远对焦。鼠标移到上方：最小对焦（CRC 系统）。

图 14 显示了计算出的 16 毫米鱼眼最小视差点的投影、畸变和偏移（蓝色曲线）。

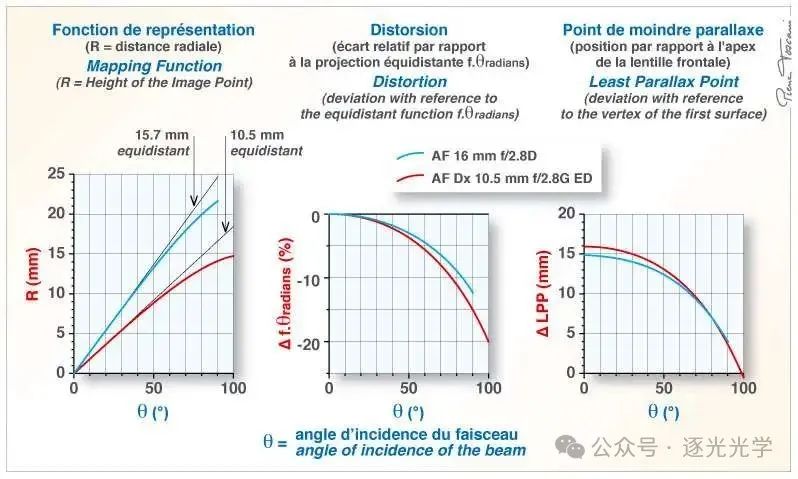
图 14 ： AF 鱼眼尼克尔 16mm f/2.8D。投影、失真和最小视差点位置（无限远对焦）。

该透镜的映射函数也是等立体类型：

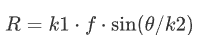
其中 k1≈1.77 和 1/k2 ≈ 0.57。

我在此稍作停顿，重点介绍一下这款等立体 16 毫米鱼眼镜头与（例如）经典的尼康 15 毫米 f/5.6（透视投影）镜头之间的区别。两者的焦距非常接近，但后者的光学系统更加复杂，视场角也更窄（110°）。图 15（下图）展示了它的投影曲线：这款镜头在 110° 视场角范围内几乎呈球面投影。

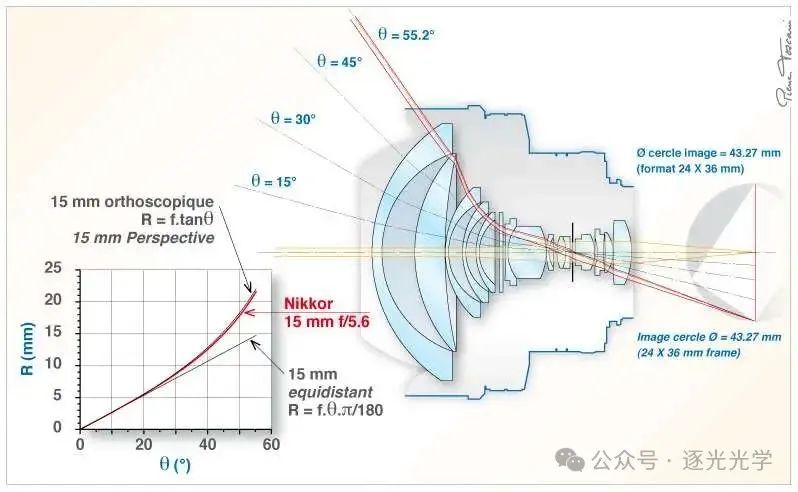
图 15 ： 尼克尔 15 mm f/5.6。简化截面和映射函数（无限远对焦）。

为了再次进行比较，图 16 展示了 15 mm f/5.6 入瞳的行为。入瞳的偏移与鱼眼镜头的偏移完全不同：在这里，我们可以观察到向后倾斜。

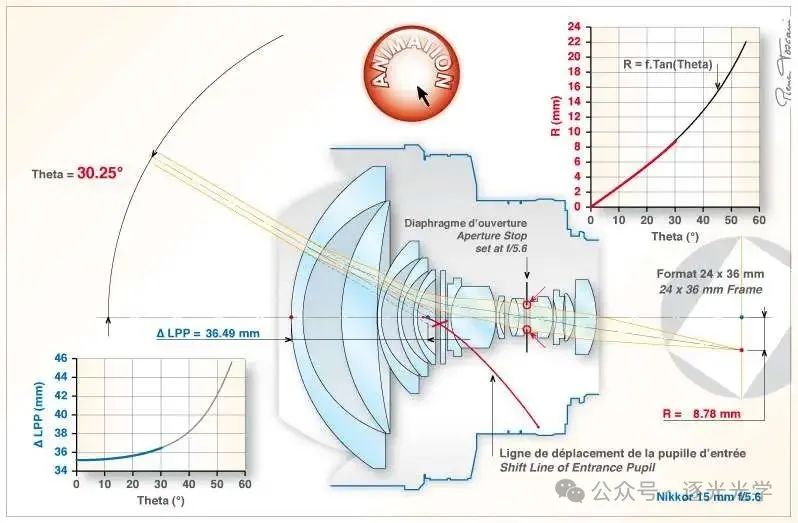
图 16 ： 尼克尔 15 mm f/5.6。入瞳位置与 Theta 角（焦点位于无穷远处）的关系。

请注意，只要角度  < 33°，孔径光阑就是唯一限制入射光束大小的因素。当角度 > 33° 时，其他元件的边缘（见红色箭头）比孔径光阑的限制作用更大（光学渐晕）。

图 16a（下图）展示了入瞳行为的另一个示例（AF-Nikkor 28 mm f/2.8D）。

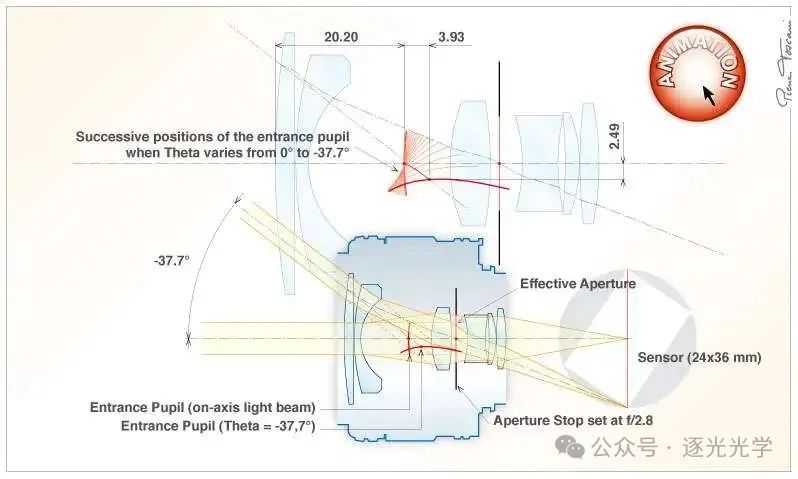
图 16a  ：AF-Nikkor 28 mm f/2.8D。入瞳位置与θ角（焦点位于无穷远处）的关系。

4 鱼眼尼克尔 6 mm f/2.8。

只是出于好奇……

这款镜头的光学系统不仅因为其尺寸令人印象深刻——前两个弯月面的有效直径分别为 213 毫米（8.4 英寸）和 100 毫米（4 英寸），前镜片顶点与像平面之间的距离为 208 毫米（8.2 英寸），还因为前三个弯月面均采用 BK7 玻璃制成。

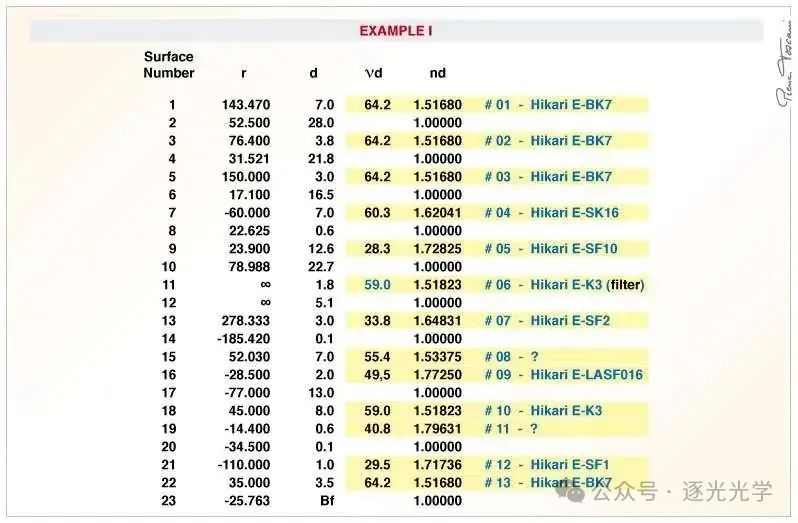
图 17 ： 鱼眼尼克尔 6 mm f/2.8。光学系统定义（黑色数据取自美国专利 3,737,214）。

下图取自 Shimizu 先生申请的 美国专利 3,737,214 号 数据（示例 1 ）（1973 年 6 月 5 日）。

这款非典型镜头的第一个版本于 1972 年 3 月发布。由于其直径为 236 毫米，重量超过 5 公斤（11 磅），价格高得离谱，很少有摄影师有机会（或有幸）使用它！

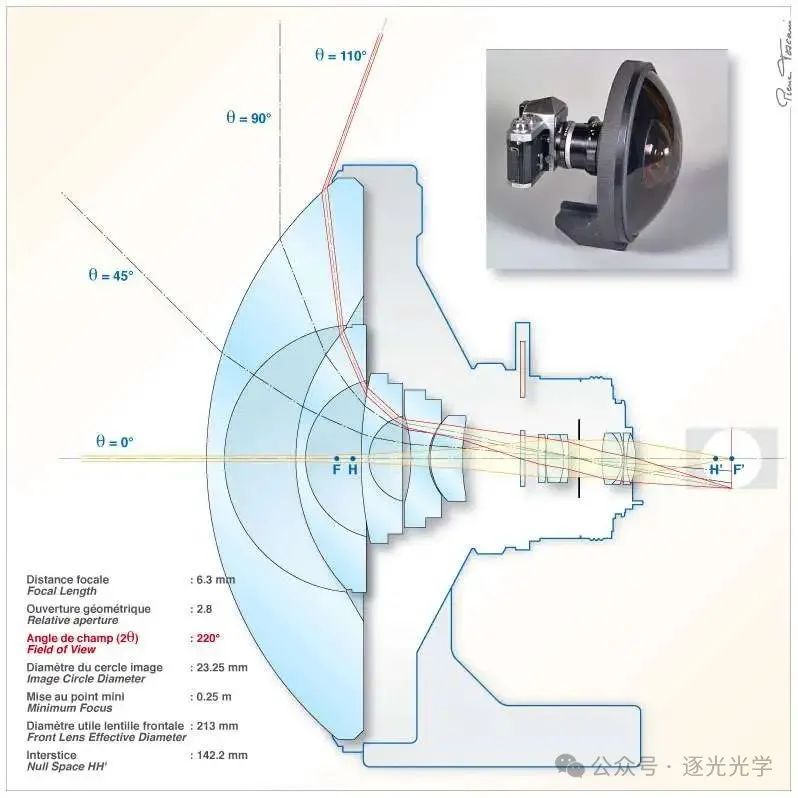
图 18 ： 尼克尔 6 mm f/2.8 鱼眼镜头。简化剖面图，全开光圈，无限远对焦。注意θ = 0°和θ= 110°时照明开口锥体之间的细微差别（暗角非常低）。

图 19（下图）的图表显示了 6 mm f/2.8 鱼眼镜头的计算投影和畸变。在 Theta = 110° 时，畸变略高于 3% ，该镜头的映射函数几乎属于等距投影类型。在 24 x 36 mm 的传感器上，圆形图像的直径略大于 23 mm。

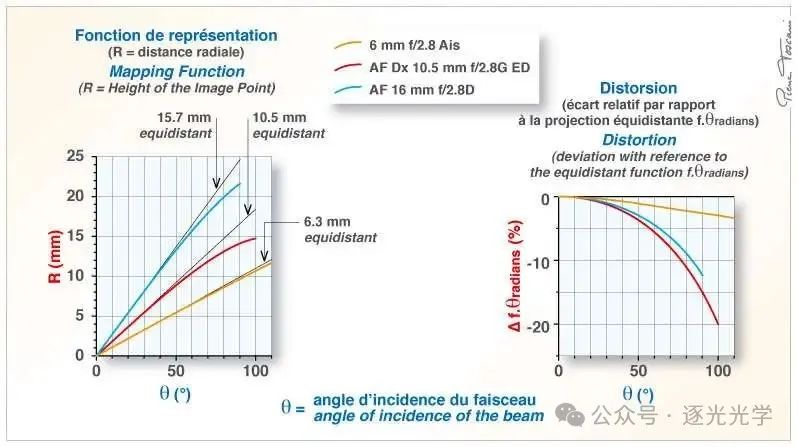
图 19 ： 鱼眼尼克尔 6 毫米 f/2.8。投影和畸变（无限远对焦）。

5 本可以是“Fisheye-Nikkor 5.4 mm f/5.6”的镜头。

另一个好奇心…

1970 年 8 月，日本光学工业株式会社（Nippon Kogaku KK）的一色先生和松木先生在美国申请了两款鱼眼镜头的专利（美国专利号 3,524,697）。这两款鱼眼镜头的视场角分别为 220° 和 270°。但均未实现量产。它们的设计非常相似；两种光学系统的主要区别在于覆盖在第二个鱼眼镜头上的巨大发散弯月面。

我选择把注意力集中在第二个“超广角”鱼眼镜头上一段时间……正如专利中所示，这款镜头的光学定义相当模糊：通常，光学系统是根据其有效焦距来定义的，或者，根据焦距 1（有时是 100）来定义的。这里我们有 10……

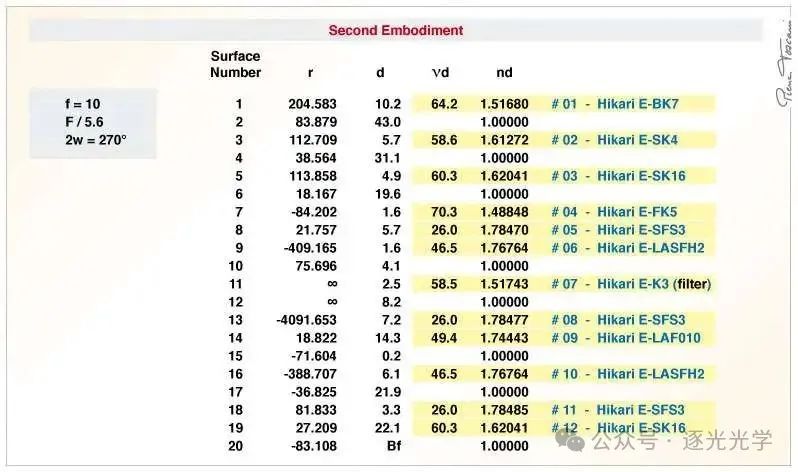
图20 ： 270°鱼眼。光学系统定义（黑色数据取自美国专利3,524,697）。

现在，焦距为 10 毫米的镜头恰好可以覆盖 24 x 36 毫米的全画幅画幅。这看起来似乎非常合理。然而，考虑到其有效直径 349 毫米的前弯月面（超过 13.7 英寸），重量超过 11 公斤（24 磅 – BK7 镜片），这款鱼眼镜头的体积实在太大了！此外，其 41.6 毫米的后镜组直径使其无法装入标准单反相机的反光腔内。

因此，如果这款镜头真的量产，它很有可能是一款鱼眼镜头，能够呈现出适合 24 x 36 mm 画幅的圆形图像。如此变换专利数据，我们得到了一款尺寸更合理的 5.4 mm f/5.6 镜头，其后焦距为 12.34 mm，后部光学元件有效直径为 22.5 mm，成像圈直径为 23.5 mm。

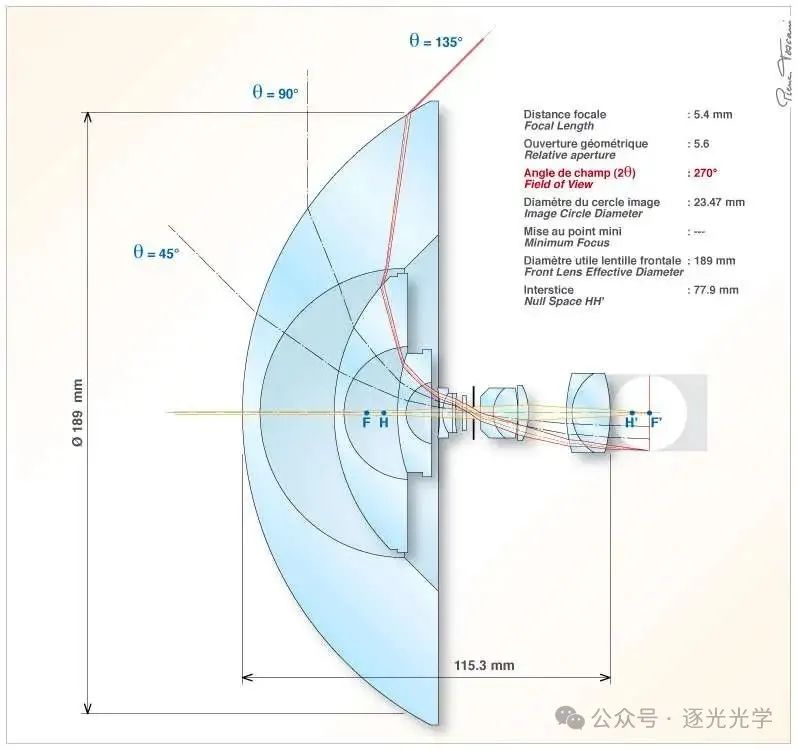
图21 ： 5.4毫米f/5.6鱼眼镜头（尼康专利）。光学系统简化部分（全光圈，无限远对焦）。

考虑到巨大的视场角，这款 5.4 毫米 f/5.6 鱼眼镜头的畸变程度相当显著……

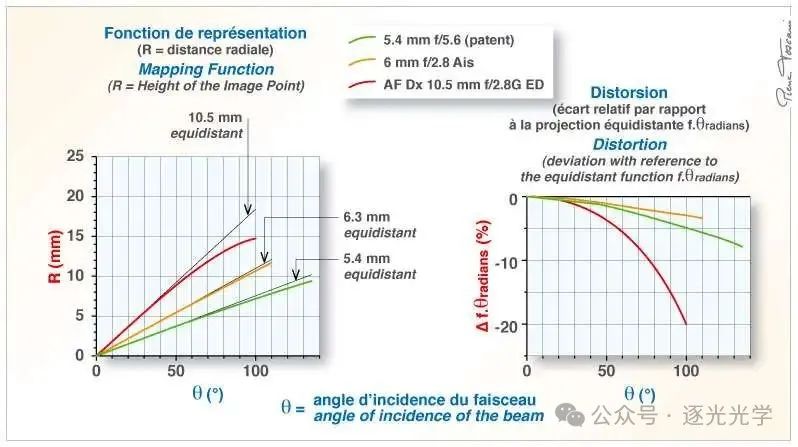
图22 ： 5.4毫米f/5.6鱼眼镜头（尼康专利）。映射函数和畸变（无限远对焦）。

毫无疑问，凭借这样的特点，这款鱼眼镜头多年来一直占据着尼康产品目录的头版……